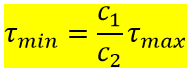[Summary] Torsion and Angle of Twist in Shafts

First: Torsion

Torsion in members of circular cross section area such as shafts occurs when these members are subjected to twisting couples (i.e. two torques "T" having the same magnitudes but opposite senses as shown above). This torsion can be calculate from the following equation:

Note that: Shafts can be either solid or hollow. In a hollow shaft, the maximum torque (and therefore, the maximum shearing stress) occurs on the outer surface, and the minimum torque (and therefore, the minimum shearing stress) occurs on the inner surface. This is shown in the following image 

Image source: F. Beer. Mechanics of Materials, Sixth Edition

Therefore; the minimum shearing stress in a hollow shaft could be calculated from the following equation:  

The polar moment of inertia can be calculated from the following equations

1. In the case of a solid circular shaft of radius c. The polar moment of inertia is
   

   

   Image source: F. Beer. Mechanics of Materials, Sixth Edition

   
   
2. In the case of a hollow circular shaft of inner radius c1 and outer radius c2, The polar moment of inertia is  

   

   Image source: F. Beer. Mechanics of Materials, Sixth Edition
   
   

Second: Angle of twist

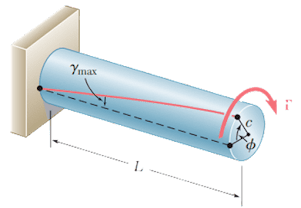Image source: F. Beer. Mechanics of Materials, Sixth Edition

When a torsion is applied to a shaft, a twist angle will form as shown above. This angle can be calculated from the following equation:

Then, we change from Radians to degrees according to the following correlation:

Similarly, we can convert from degrees to Radians

[Important] A bonus

If you use flashcards in your studies, you might find our "compact flashcards" interesting. Visit our board "Informative Compact Flashcards" on Pinterest, and get access to informative and ready to study flashcards for FREE!!  (Click Here)

Resources:

• F. Beer. "Mechanics of Materials," Sixth Edition