A beam is said to be in pure bending if is subjected to equal and opposite couples M and M' acting in the same longitudinal plane. The member will then bend under the action of the couples as shown in the following figure:
 |
| Image source: F. Beer. "Mechanics of Materials," Sixth Edition |
The bending stress
The bending stress which is maximum on the surface and minimum in the center can be calculated from the following equation:
The radius of curvature "R"
The radius of curvature "R" can be calculated from the following equation:
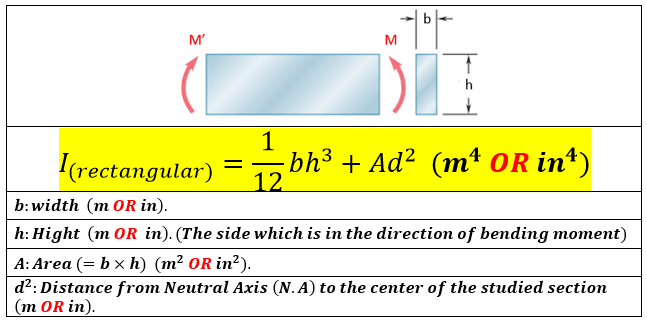
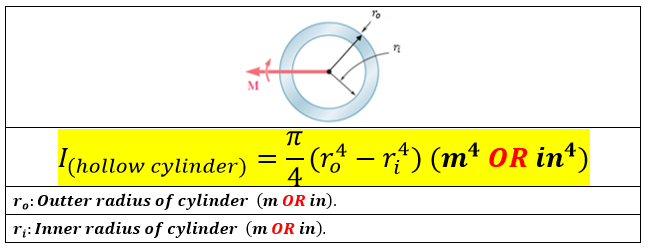
The Area moment of inertia "I"
- The Area Moment of Inertia for a rectangular section can be calculated from:
- The Area Moment of Inertia for a solid cylindrical section can be calculated from:
- The Area Moment of Inertia for a hollow cylindrical section can be calculated from:
The Neutral Axis (N.A)
For symmetrical shapes, the neutral axis is the line that passes through the center of the shape as shown below:
If the shape is formed of many unsymmetrical parts or parts of different dimensions - as shown below, we then must use the "Centroid" to locate the position of neutral axis as shown below:
 |
| Image source: F. Beer. "Mechanics of Materials," Sixth Edition |
Sample problem 4.2 in the book: F. Beer. "Mechanics of Materials," Sixth Edition, represents a good example of how to use the centroid.
[Important] A bonus
If you use flashcards in your studies, you might find our "compact flashcards" interesting. Visit our board "Informative Compact Flashcards" on Pinterest, and get access to informative and ready to study flashcards for FREE!! (Click Here)
Resources:
- F. Beer. "Mechanics of Materials," Sixth Edition
